Gradient Tape

Forståelse af grundlæggende tensoroperationer muliggør videreudvikling til at effektivisere og accelerere disse processer ved hjælp af indbyggede TensorFlow-funktioner. Det første af disse avancerede værktøjer, der udforskes, er Gradient Tape.

Hvad er Gradient Tape?

Dette kapitel går i dybden med et af de grundlæggende begreber i TensorFlow, Gradient Tape. Denne funktion er afgørende for forståelse og implementering af gradientbaserede optimeringsteknikker, især inden for deep learning.

Gradient Tape i TensorFlow er et værktøj, der registrerer operationer til automatisk differentiering. Når operationer udføres inden for et Gradient Tape-blok, registrerer TensorFlow alle de beregninger, der foretages. Dette er særligt nyttigt ved træning af maskinlæringsmodeller, hvor gradienter er nødvendige for at optimere modelparametre.

Bemærk

Grundlæggende er en gradient et sæt af partielle afledte.

Anvendelse af Gradient Tape

For at bruge Gradient Tape, følg disse trin:

Opret et Gradient Tape-blok: brug with tf.GradientTape() as tape:. Inde i denne blok spores alle beregninger;
Definér beregningerne: udfør operationer med tensorer inden for blokken (f.eks. definér et fremadrettet pass af et neuralt netværk);
Beregn gradienter: brug tape.gradient(target, sources) for at beregne gradienterne af målet med hensyn til kilderne.

Simpel gradientberegning

Et simpelt eksempel for bedre forståelse.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Denne kode beregner gradienten af y = x^2 ved x = 3. Dette svarer til den partielle afledte af y med hensyn til x.

Flere partielle afledte

Når output påvirkes af flere input, kan en partiel afledt beregnes med hensyn til hver af disse input (eller blot nogle udvalgte). Dette opnås ved at angive en liste af variable som parameteren sources.

Outputtet fra denne operation vil være en tilsvarende liste af tensorer, hvor hver tensor repræsenterer den partielle afledte med hensyn til hver af de variable, der er angivet i sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Denne kode beregner gradienten af funktionen y = sum(x^2 + 2*z) for givne værdier af x og z. I dette eksempel vises gradienten af x som en 2D-tensor, hvor hvert element svarer til den partielle afledte af den respektive værdi i den oprindelige x-matrix.

Eksempelbeskrivelse

Beregning af gradienten med hensyn til x

Når vi beregner den afledte af y med hensyn til x, spørger vi i bund og grund: "Hvis vi ændrer værdien af x en smule, hvor meget ændrer y sig så?" Operationen på x er opløftning i anden (x^2), så den afledte fortæller os, at for hver enheds forøgelse i x, vil y stige med 2*x.

Da alle elementer i x er 3.0:

Hvert elements gradient er 2*3.0 = 6.0;
Gradientmatricen med hensyn til x har samme form som x selv (2x3), hvor hvert element er 6.0. Dette indikerer, at en forøgelse af et enkelt element i x med 1 vil øge y med 6 enheder.

Beregning af gradienten med hensyn til z

For z ser vi på, hvordan ændringer i z påvirker y. Da z lægges til hvert kvadreret element af x (efter fordobling), spørger vi i praksis: "Hvis z øges med 1, hvor meget øges y så?" Ifølge reglerne for broadcasting lægges 2*z til hvert element i x^2, som om vi havde en matrix på samme størrelse som x, fyldt med 2*z.

Operationen 2*z med hensyn til z er ligetil: dens afledte er 2, fordi 2*z ændres med 2 enheder for hver enhedsændring i z;
Da denne operation påvirker hvert element i matricen x, er den samlede ændring i y for en enhedsændring i z 2 gange antallet af elementer i x (som er 6, fra 2x3 matricen). Den samlede gradient med hensyn til z er altså 2*6 = 12. Det betyder, at en forøgelse af z med 1 enhed øger y med 12 enheder, hvilket afspejler den samlede effekt af ændringen på tværs af alle elementer i x.

Sammenfatning

Gradienten med hensyn til x er en matrix, der viser, hvordan en enheds forøgelse i et hvilket som helst element af x fører til en 6-enheds forøgelse i y, hvilket afspejler det direkte forhold mellem ændringer i x og ændringer i y;
Gradienten med hensyn til z er en skalar (12), der viser den samlede effekt af en enheds forøgelse i z på y, idet der tages højde for virkningen på hele matricen x.

Bemærk

For yderligere indsigt i Gradient Tape-funktioner, herunder højere ordens afledte og udtrækning af Jacobian-matricen, henvises til den officielle TensorFlow documentation.

Opgave

Swipe to start coding

Dit mål er at beregne gradienten (den afledte) af en given matematisk funktion på et specificeret punkt ved hjælp af TensorFlows Gradient Tape. Funktionen og punktet vil blive angivet, og du vil se, hvordan TensorFlow bruges til at finde gradienten på dette punkt.

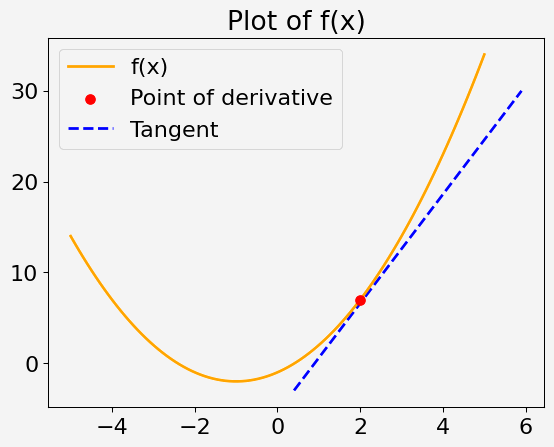
Overvej en kvadratisk funktion af en enkelt variabel x, defineret som:

f(x) = x^2 + 2x - 1

Din opgave er at beregne den afledte af denne funktion ved x = 2.