Gradient-Tape

Gradient Tape

Das Verständnis grundlegender Tensor-Operationen ermöglicht es, diese Prozesse mithilfe von integrierten TensorFlow-Funktionen zu optimieren und zu beschleunigen. Das erste dieser fortgeschrittenen Werkzeuge, das betrachtet wird, ist das Gradient Tape.

Was ist Gradient Tape?

Dieses Kapitel behandelt eines der grundlegenden Konzepte in TensorFlow, das Gradient Tape. Diese Funktion ist entscheidend für das Verständnis und die Implementierung von gradientenbasierten Optimierungstechniken, insbesondere im Deep Learning.

Gradient Tape in TensorFlow ist ein Werkzeug, das Operationen für die automatische Differenzierung aufzeichnet. Wenn Operationen innerhalb eines Gradient Tape-Blocks ausgeführt werden, verfolgt TensorFlow alle durchgeführten Berechnungen. Dies ist besonders nützlich beim Trainieren von Machine-Learning-Modellen, bei denen Gradienten zur Optimierung der Modellparameter benötigt werden.

Hinweis

Im Wesentlichen ist ein Gradient eine Menge von partiellen Ableitungen.

Verwendung von Gradient Tape

Für die Nutzung von Gradient Tape sind folgende Schritte erforderlich:

Erstellen eines Gradient Tape-Blocks: Verwenden von with tf.GradientTape() as tape:. Innerhalb dieses Blocks werden alle Berechnungen aufgezeichnet;
Definition der Berechnungen: Ausführen von Operationen mit Tensoren innerhalb des Blocks (z. B. Definition eines Forward-Passes eines neuronalen Netzes);
Berechnung der Gradienten: Verwenden von tape.gradient(target, sources), um die Gradienten des Ziels in Bezug auf die Quellen zu berechnen.

Einfache Gradientenberechnung

Ein einfaches Beispiel zur besseren Veranschaulichung.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Dieser Code berechnet das Gradienten von y = x^2 bei x = 3. Dies entspricht der partiellen Ableitung von y bezüglich x.

Mehrere partielle Ableitungen

Wenn das Ergebnis von mehreren Eingaben beeinflusst wird, kann eine partielle Ableitung bezüglich jeder dieser Eingaben (oder nur ausgewählter) berechnet werden. Dies geschieht durch Angabe einer Liste von Variablen als sources-Parameter.

Das Ergebnis dieser Operation ist eine entsprechende Liste von Tensoren, wobei jeder Tensor die partielle Ableitung bezüglich einer der in sources angegebenen Variablen darstellt.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Dieser Code berechnet das Gradientenfeld der Funktion y = sum(x^2 + 2*z) für gegebene Werte von x und z. In diesem Beispiel wird der Gradient von x als 2D-Tensor dargestellt, wobei jedes Element der partiellen Ableitung des jeweiligen Werts in der ursprünglichen x-Matrix entspricht.

Beispielbeschreibung

Berechnung des Gradienten bezüglich x

Wenn wir die Ableitung von y nach x berechnen, fragen wir im Wesentlichen: „Wenn wir den Wert von x ein wenig ändern, wie stark ändert sich dann y?“ Die Operation auf x ist das Quadrieren (x^2), daher sagt uns die Ableitung, dass sich x für jede Einheitserhöhung von y um 2*x erhöht.

Da alle Elemente von x den Wert 3.0 haben:

Der Gradient jedes Elements beträgt 2*3.0 = 6.0;
Die Gradientenmatrix bezüglich x hat die gleiche Form wie x selbst (2x3), wobei jedes Element 6.0 ist. Dies zeigt, dass eine Erhöhung eines einzelnen Elements von x um 1 zu einer Erhöhung von y um 6 Einheiten führt.

Berechnung des Gradienten bezüglich z

Für z betrachten wir, wie Änderungen in z y beeinflussen. Da z zu jedem quadrierten Element von x (nach der Verdopplung) addiert wird, fragen wir im Grunde: „Wenn z um 1 erhöht wird, wie stark erhöht sich dann y?“ Nach den Regeln des Broadcastings wird 2*z zu jedem Element von x^2 addiert, als hätten wir eine Matrix in der gleichen Größe wie x, gefüllt mit 2*z.

Die Operation 2*z bezüglich z ist einfach: Die Ableitung ist 2, da sich 2*z für jede Einheitserhöhung von z um 2 Einheiten ändert;
Da diese Operation jedoch jedes Element der Matrix x betrifft, beträgt die Gesamtänderung von y für eine Einheitserhöhung von z 2 mal die Anzahl der Elemente in x (also 6, aus der 2x3-Matrix). Somit beträgt der gesamte Gradient bezüglich z 2*6 = 12. Das bedeutet, dass eine Erhöhung von z um 1 Einheit zu einer Erhöhung von y um 12 Einheiten führt, was den kombinierten Effekt der Änderung über alle Elemente von x widerspiegelt.

Zusammenfassung

Der Gradient bezüglich x ist eine Matrix, die zeigt, wie eine Einheitserhöhung eines beliebigen Elements von x zu einer Erhöhung von y um 6 Einheiten führt, was die direkte Beziehung zwischen Änderungen in x und Änderungen in y widerspiegelt;
Der Gradient bezüglich z ist ein Skalar (12), der die Gesamtauswirkung einer Einheitserhöhung von z auf y zeigt, wobei der Einfluss auf die gesamte Matrix x berücksichtigt wird.

Hinweis

Weitere Informationen zu den Gradient Tape-Funktionen, einschließlich höherer Ableitungen und der Extraktion der Jacobi-Matrix, finden Sie in der offiziellen TensorFlow documentation.

War alles klar?

Danke für Ihr Feedback!

Abschnitt 3. Kapitel 2

single

Swipe um das Menü anzuzeigen

Gradient Tape

Was ist Gradient Tape?

Hinweis

Im Wesentlichen ist ein Gradient eine Menge von partiellen Ableitungen.

Verwendung von Gradient Tape

Für die Nutzung von Gradient Tape sind folgende Schritte erforderlich:

Erstellen eines Gradient Tape-Blocks: Verwenden von with tf.GradientTape() as tape:. Innerhalb dieses Blocks werden alle Berechnungen aufgezeichnet;
Definition der Berechnungen: Ausführen von Operationen mit Tensoren innerhalb des Blocks (z. B. Definition eines Forward-Passes eines neuronalen Netzes);
Berechnung der Gradienten: Verwenden von tape.gradient(target, sources), um die Gradienten des Ziels in Bezug auf die Quellen zu berechnen.

Einfache Gradientenberechnung

Ein einfaches Beispiel zur besseren Veranschaulichung.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Dieser Code berechnet das Gradienten von y = x^2 bei x = 3. Dies entspricht der partiellen Ableitung von y bezüglich x.

Mehrere partielle Ableitungen

Das Ergebnis dieser Operation ist eine entsprechende Liste von Tensoren, wobei jeder Tensor die partielle Ableitung bezüglich einer der in sources angegebenen Variablen darstellt.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Beispielbeschreibung

Berechnung des Gradienten bezüglich x

Da alle Elemente von x den Wert 3.0 haben:

Der Gradient jedes Elements beträgt 2*3.0 = 6.0;
Die Gradientenmatrix bezüglich x hat die gleiche Form wie x selbst (2x3), wobei jedes Element 6.0 ist. Dies zeigt, dass eine Erhöhung eines einzelnen Elements von x um 1 zu einer Erhöhung von y um 6 Einheiten führt.

Berechnung des Gradienten bezüglich z

Die Operation 2*z bezüglich z ist einfach: Die Ableitung ist 2, da sich 2*z für jede Einheitserhöhung von z um 2 Einheiten ändert;
Da diese Operation jedoch jedes Element der Matrix x betrifft, beträgt die Gesamtänderung von y für eine Einheitserhöhung von z 2 mal die Anzahl der Elemente in x (also 6, aus der 2x3-Matrix). Somit beträgt der gesamte Gradient bezüglich z 2*6 = 12. Das bedeutet, dass eine Erhöhung von z um 1 Einheit zu einer Erhöhung von y um 12 Einheiten führt, was den kombinierten Effekt der Änderung über alle Elemente von x widerspiegelt.

Zusammenfassung

Der Gradient bezüglich x ist eine Matrix, die zeigt, wie eine Einheitserhöhung eines beliebigen Elements von x zu einer Erhöhung von y um 6 Einheiten führt, was die direkte Beziehung zwischen Änderungen in x und Änderungen in y widerspiegelt;
Der Gradient bezüglich z ist ein Skalar (12), der die Gesamtauswirkung einer Einheitserhöhung von z auf y zeigt, wobei der Einfluss auf die gesamte Matrix x berücksichtigt wird.

Hinweis

Weitere Informationen zu den Gradient Tape-Funktionen, einschließlich höherer Ableitungen und der Extraktion der Jacobi-Matrix, finden Sie in der offiziellen TensorFlow documentation.

Aufgabe

Wischen, um mit dem Codieren zu beginnen

Ihr Ziel ist es, die Ableitung (Gradient) einer gegebenen mathematischen Funktion an einem bestimmten Punkt mithilfe von TensorFlows Gradient Tape zu berechnen. Die Funktion und der Punkt werden vorgegeben, und Sie erfahren, wie Sie TensorFlow verwenden, um den Gradienten an diesem Punkt zu bestimmen.

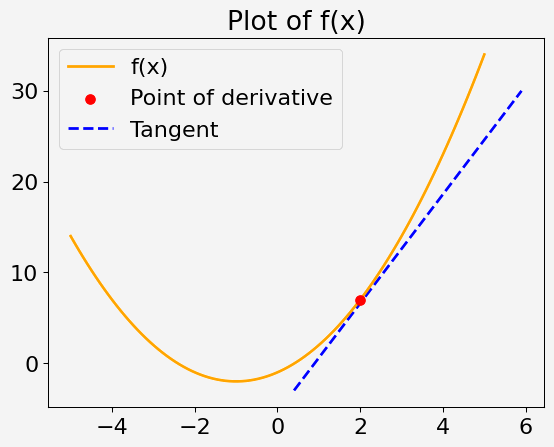
Betrachten Sie eine quadratische Funktion einer einzelnen Variablen x, definiert als:

f(x) = x^2 + 2x - 1

Ihre Aufgabe ist es, die Ableitung dieser Funktion bei x = 2 zu berechnen.

Schritte

Definieren Sie die Variable x an dem Punkt, an dem Sie die Ableitung berechnen möchten.
Verwenden Sie Gradient Tape, um die Berechnung der Funktion f(x) aufzuzeichnen.
Berechnen Sie den Gradienten von f(x) am angegebenen Punkt.

Hinweis

Der Gradient kann nur für Werte vom Fließkommatyp berechnet werden.

Lösung

Wechseln Sie zum Desktop, um in der realen Welt zu übenFahren Sie dort fort, wo Sie sind, indem Sie eine der folgenden Optionen verwenden

War alles klar?

Danke für Ihr Feedback!

Abschnitt 3. Kapitel 2

single

Fragen Sie AI

Fragen Sie alles oder probieren Sie eine der vorgeschlagenen Fragen, um unser Gespräch zu beginnen