single
 Cinta de Gradiente
Cinta de Gradiente
Desliza para mostrar el menú
Cinta de Gradiente
Comprender las operaciones fundamentales con tensores permite avanzar hacia la optimización y aceleración de estos procesos utilizando funcionalidades integradas de TensorFlow. La primera de estas herramientas avanzadas a explorar es la Cinta de Gradiente.
¿Qué es la Cinta de Gradiente?
Este capítulo aborda uno de los conceptos fundamentales en TensorFlow, la Cinta de Gradiente. Esta funcionalidad es esencial para comprender e implementar técnicas de optimización basada en gradientes, especialmente en aprendizaje profundo.
La Cinta de Gradiente en TensorFlow es una herramienta que registra operaciones para la diferenciación automática. Cuando se realizan operaciones dentro de un bloque de Cinta de Gradiente, TensorFlow rastrea todos los cálculos que se ejecutan. Esto resulta especialmente útil para el entrenamiento de modelos de aprendizaje automático, donde se requieren gradientes para optimizar los parámetros del modelo.
Esencialmente, un gradiente es un conjunto de derivadas parciales.
Uso de Gradient Tape
Para utilizar Gradient Tape, siga estos pasos:
- Crear un bloque de Gradient Tape: use
with tf.GradientTape() as tape:. Dentro de este bloque, se rastrean todos los cálculos; - Definir los cálculos: realice operaciones con tensores dentro del bloque (por ejemplo, defina una pasada hacia adelante de una red neuronal);
- Calcular los gradientes: use
tape.gradient(target, sources)para calcular los gradientes del objetivo con respecto a las fuentes.
Cálculo simple de gradiente
Un ejemplo sencillo para comprenderlo mejor.
123456789101112131415import tensorflow as tf # Define input variables x = tf.Variable(3.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = x * x # Extract the gradient for the specific input (`x`) grad = tape.gradient(y, x) print(f'Result of y: {y}') print(f'The gradient of y with respect to x is: {grad.numpy()}')
Este código calcula el gradiente de y = x^2 en x = 3. Esto es equivalente a la derivada parcial de y con respecto a x.
Varias Derivadas Parciales
Cuando la salida está influenciada por múltiples entradas, se puede calcular una derivada parcial con respecto a cada una de estas entradas (o solo algunas seleccionadas). Esto se logra proporcionando una lista de variables como el parámetro sources.
La salida de esta operación será una lista correspondiente de tensores, donde cada tensor representa la derivada parcial con respecto a cada una de las variables especificadas en sources.
1234567891011121314151617import tensorflow as tf # Define input variables x = tf.Variable(tf.fill((2, 3), 3.0)) z = tf.Variable(5.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = tf.reduce_sum(x * x + 2 * z) # Extract the gradient for the specific inputs (`x` and `z`) grad = tape.gradient(y, [x, z]) print(f'Result of y: {y}') print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}") print(f"The gradient of y with respect to z is: {grad[1].numpy()}")
Este código calcula el gradiente de la función y = sum(x^2 + 2*z) para valores dados de x y z. En este ejemplo, el gradiente de x se muestra como un tensor 2D, donde cada elemento corresponde a la derivada parcial del valor respectivo en la matriz original x.
Para obtener información adicional sobre las capacidades de Gradient Tape, incluyendo derivadas de orden superior y la extracción de la matriz Jacobiana, consulte la documentación oficial de TensorFlow.
Swipe to start coding
El objetivo es calcular el gradiente (derivada) de una función matemática dada en un punto específico utilizando Gradient Tape de TensorFlow. Se proporcionarán la función y el punto, y verás cómo usar TensorFlow para encontrar el gradiente en ese punto.
Considera una función cuadrática de una sola variable x, definida como:
f(x) = x^2 + 2x - 1
La tarea consiste en calcular la derivada de esta función en x = 2.
Pasos
- Definir la variable
xen el punto donde se desea calcular la derivada. - Utilizar Gradient Tape para registrar el cálculo de la función
f(x). - Calcular el gradiente de
f(x)en el punto especificado.
Nota
El gradiente solo puede calcularse para valores de tipo de punto flotante.
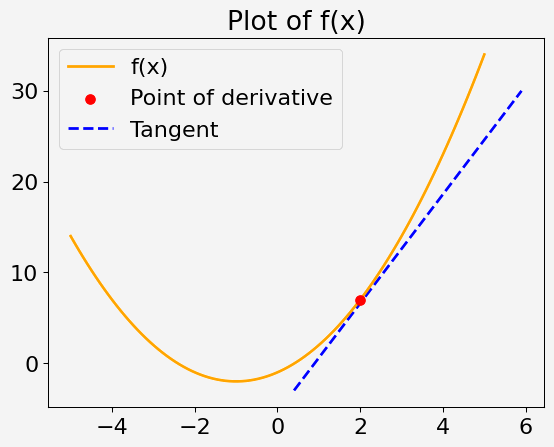
Solución
¡Gracias por tus comentarios!
single
Pregunte a AI
Pregunte a AI

Pregunte lo que quiera o pruebe una de las preguntas sugeridas para comenzar nuestra charla