Gradient Tape

La compréhension des opérations fondamentales sur les tenseurs permet de passer à l’optimisation et à l’accélération de ces processus à l’aide des fonctionnalités intégrées de TensorFlow. Le premier de ces outils avancés à explorer est le Gradient Tape.

Qu’est-ce que le Gradient Tape ?

Ce chapitre aborde l’un des concepts fondamentaux de TensorFlow, le Gradient Tape. Cette fonctionnalité est essentielle pour comprendre et mettre en œuvre des techniques d’optimisation basées sur le gradient, en particulier dans l’apprentissage profond.

Le Gradient Tape dans TensorFlow est un outil qui enregistre les opérations pour la différentiation automatique. Lorsque des opérations sont effectuées à l’intérieur d’un bloc Gradient Tape, TensorFlow suit toutes les opérations de calcul effectuées. Ceci est particulièrement utile lors de l’entraînement de modèles d’apprentissage automatique, où les gradients sont nécessaires pour optimiser les paramètres du modèle.

Remarque

Essentiellement, un gradient est un ensemble de dérivées partielles.

Utilisation de Gradient Tape

Pour utiliser Gradient Tape, suivre les étapes suivantes :

Créer un bloc Gradient Tape : utiliser with tf.GradientTape() as tape:. Toutes les opérations à l'intérieur de ce bloc sont enregistrées ;
Définir les calculs : effectuer des opérations avec des tenseurs dans le bloc (par exemple, définir une passe avant d'un réseau de neurones) ;
Calculer les gradients : utiliser tape.gradient(target, sources) pour calculer les gradients de la cible par rapport aux sources.

Calcul de gradient simple

Un exemple simple pour mieux comprendre.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Ce code calcule le gradient de y = x^2 en x = 3. Cela correspond à la dérivée partielle de y par rapport à x.

Plusieurs dérivées partielles

Lorsque la sortie est influencée par plusieurs entrées, une dérivée partielle peut être calculée par rapport à chacune de ces entrées (ou seulement à certaines d'entre elles). Ceci est réalisé en fournissant une liste de variables comme paramètre sources.

Le résultat de cette opération sera une liste correspondante de tenseurs, où chaque tenseur représente la dérivée partielle par rapport à chacune des variables spécifiées dans sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Ce code calcule le gradient de la fonction y = sum(x^2 + 2*z) pour des valeurs données de x et z. Dans cet exemple, le gradient de x est présenté sous forme de tenseur 2D, où chaque élément correspond à la dérivée partielle de la valeur respective dans la matrice x d'origine.

Note

Pour des informations supplémentaires sur les fonctionnalités de Gradient Tape, y compris les dérivées d'ordre supérieur et l'extraction de la matrice Jacobienne, consultez la documentation TensorFlow officielle.

Tâche

Swipe to start coding

Votre objectif est de calculer le gradient (dérivée) d'une fonction mathématique donnée en un point spécifié à l'aide du Gradient Tape de TensorFlow. La fonction et le point seront fournis, et vous verrez comment utiliser TensorFlow pour trouver le gradient en ce point.

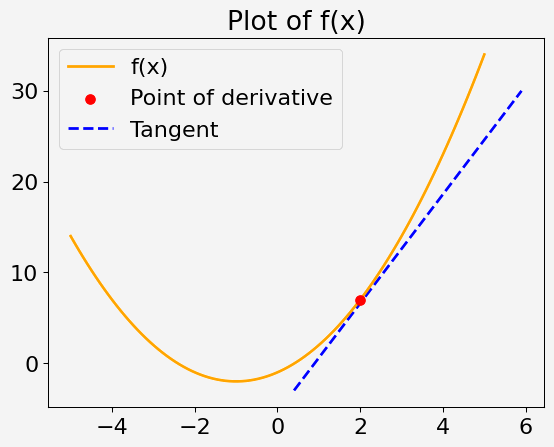
Considérons une fonction quadratique d'une seule variable x, définie comme suit :

f(x) = x^2 + 2x - 1

Votre tâche consiste à calculer la dérivée de cette fonction en x = 2.

Étapes

Définir la variable x au point où vous souhaitez calculer la dérivée.
Utiliser Gradient Tape pour enregistrer le calcul de la fonction f(x).
Calculer le gradient de f(x) au point spécifié.

Remarque

Le gradient ne peut être calculé que pour des valeurs de type flottant.

Solution

Tout était clair ?

Merci pour vos commentaires !

Section 2. Chapitre 1

single

Demandez à l'IA

Posez n'importe quelle question ou essayez l'une des questions suggérées pour commencer notre discussion

Awesome!

Completion rate improved to 5.56

Glissez pour afficher le menu

Gradient Tape

Qu’est-ce que le Gradient Tape ?

Remarque

Essentiellement, un gradient est un ensemble de dérivées partielles.

Utilisation de Gradient Tape

Pour utiliser Gradient Tape, suivre les étapes suivantes :

Créer un bloc Gradient Tape : utiliser with tf.GradientTape() as tape:. Toutes les opérations à l'intérieur de ce bloc sont enregistrées ;
Définir les calculs : effectuer des opérations avec des tenseurs dans le bloc (par exemple, définir une passe avant d'un réseau de neurones) ;
Calculer les gradients : utiliser tape.gradient(target, sources) pour calculer les gradients de la cible par rapport aux sources.

Calcul de gradient simple

Un exemple simple pour mieux comprendre.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Ce code calcule le gradient de y = x^2 en x = 3. Cela correspond à la dérivée partielle de y par rapport à x.

Plusieurs dérivées partielles

Le résultat de cette opération sera une liste correspondante de tenseurs, où chaque tenseur représente la dérivée partielle par rapport à chacune des variables spécifiées dans sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Note

Tâche

Swipe to start coding

Considérons une fonction quadratique d'une seule variable x, définie comme suit :

f(x) = x^2 + 2x - 1

Votre tâche consiste à calculer la dérivée de cette fonction en x = 2.

Étapes

Définir la variable x au point où vous souhaitez calculer la dérivée.
Utiliser Gradient Tape pour enregistrer le calcul de la fonction f(x).
Calculer le gradient de f(x) au point spécifié.

Remarque

Le gradient ne peut être calculé que pour des valeurs de type flottant.

Solution

Passez à un bureau pour une pratique réelleContinuez d'où vous êtes en utilisant l'une des options ci-dessous

Tout était clair ?

Merci pour vos commentaires !

Section 2. Chapitre 1

single

Bande de Gradient

Gradient Tape

Qu’est-ce que le Gradient Tape ?

Utilisation de Gradient Tape

Calcul de gradient simple

Plusieurs dérivées partielles

Étapes

Solution

Awesome!

Bande de Gradient

Gradient Tape

Qu’est-ce que le Gradient Tape ?

Utilisation de Gradient Tape

Calcul de gradient simple

Plusieurs dérivées partielles

Étapes

Solution