single
 Nastro del Gradiente
Nastro del Gradiente
Scorri per mostrare il menu
Gradient Tape
La comprensione delle operazioni fondamentali sui tensori consente di passare all'ottimizzazione e all'accelerazione di questi processi utilizzando le funzionalità integrate di TensorFlow. Il primo di questi strumenti avanzati da esplorare è il Gradient Tape.
Cos'è il Gradient Tape?
Questo capitolo approfondisce uno dei concetti fondamentali in TensorFlow, il Gradient Tape. Questa funzionalità è essenziale per comprendere e implementare le tecniche di ottimizzazione basate sul gradiente, in particolare nell'ambito del deep learning.
Il Gradient Tape in TensorFlow è uno strumento che registra le operazioni per la differenziazione automatica. Quando le operazioni vengono eseguite all'interno di un blocco Gradient Tape, TensorFlow tiene traccia di tutti i calcoli effettuati. Questo risulta particolarmente utile nell'addestramento dei modelli di machine learning, dove sono necessari i gradienti per ottimizzare i parametri del modello.
Fondamentalmente, un gradiente è un insieme di derivate parziali.
Utilizzo di Gradient Tape
Per utilizzare Gradient Tape, seguire questi passaggi:
- Creare un blocco Gradient Tape: utilizzare
with tf.GradientTape() as tape:. All'interno di questo blocco, tutti i calcoli vengono tracciati; - Definire i calcoli: eseguire operazioni con i tensori all'interno del blocco (ad esempio, definire un passaggio in avanti di una rete neurale);
- Calcolare i gradienti: utilizzare
tape.gradient(target, sources)per calcolare i gradienti del target rispetto alle sorgenti.
Calcolo semplice del gradiente
Un esempio semplice per comprendere meglio questo concetto.
123456789101112131415import tensorflow as tf # Define input variables x = tf.Variable(3.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = x * x # Extract the gradient for the specific input (`x`) grad = tape.gradient(y, x) print(f'Result of y: {y}') print(f'The gradient of y with respect to x is: {grad.numpy()}')
Questo codice calcola il gradiente di y = x^2 in x = 3. Questo equivale alla derivata parziale di y rispetto a x.
Diverse Derivate Parziali
Quando l'output è influenzato da più input, è possibile calcolare una derivata parziale rispetto a ciascuno di questi input (o solo ad alcuni selezionati). Questo si ottiene fornendo una lista di variabili come parametro sources.
L'output di questa operazione sarà una corrispondente lista di tensori, dove ciascun tensore rappresenta la derivata parziale rispetto a ciascuna delle variabili specificate in sources.
1234567891011121314151617import tensorflow as tf # Define input variables x = tf.Variable(tf.fill((2, 3), 3.0)) z = tf.Variable(5.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = tf.reduce_sum(x * x + 2 * z) # Extract the gradient for the specific inputs (`x` and `z`) grad = tape.gradient(y, [x, z]) print(f'Result of y: {y}') print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}") print(f"The gradient of y with respect to z is: {grad[1].numpy()}")
Questo codice calcola il gradiente della funzione y = sum(x^2 + 2*z) per valori dati di x e z. In questo esempio, il gradiente di x viene mostrato come un tensore 2D, dove ogni elemento corrisponde alla derivata parziale del rispettivo valore nella matrice x originale.
Per ulteriori approfondimenti sulle funzionalità di Gradient Tape, incluse derivate di ordine superiore ed estrazione della matrice Jacobiana, consultare la documentazione TensorFlow.
Swipe to start coding
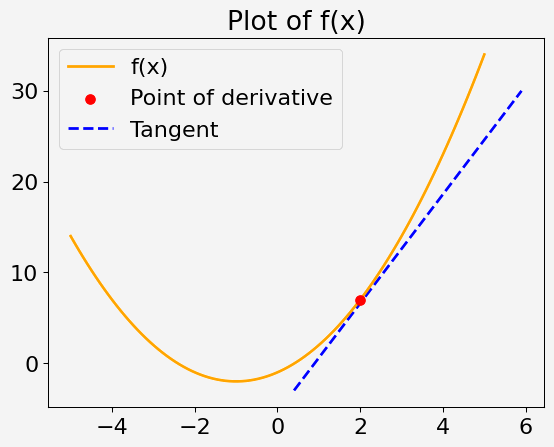
Il tuo obiettivo è calcolare il gradiente (derivata) di una data funzione matematica in un punto specificato utilizzando il Gradient Tape di TensorFlow. Verranno forniti la funzione e il punto, e vedrai come utilizzare TensorFlow per trovare il gradiente in quel punto.
Considera una funzione quadratica di una sola variabile x, definita come:
f(x) = x^2 + 2x - 1
Il tuo compito è calcolare la derivata di questa funzione in x = 2.
Passaggi
- Definire la variabile
xnel punto in cui si desidera calcolare la derivata. - Utilizzare Gradient Tape per registrare il calcolo della funzione
f(x). - Calcolare il gradiente di
f(x)nel punto specificato.
Nota
Il gradiente può essere calcolato solo per valori di tipo floating-point.
Soluzione
Grazie per i tuoi commenti!
single
Chieda ad AI
Chieda ad AI

Chieda pure quello che desidera o provi una delle domande suggerite per iniziare la nostra conversazione