Gradient Tape

Forståelse av grunnleggende tensoroperasjoner gir mulighet til å effektivisere og akselerere disse prosessene ved hjelp av innebygde TensorFlow-funksjoner. Det første av disse avanserte verktøyene som introduseres er Gradient Tape.

Hva er Gradient Tape?

Dette kapittelet tar for seg et av de grunnleggende konseptene i TensorFlow, Gradient Tape. Denne funksjonen er avgjørende for å forstå og implementere gradientbaserte optimaliseringsteknikker, spesielt innen dyp læring.

Gradient Tape i TensorFlow er et verktøy som registrerer operasjoner for automatisk derivasjon. Når operasjoner utføres innenfor en Gradient Tape-blokk, holder TensorFlow oversikt over alle beregningene som skjer. Dette er spesielt nyttig ved trening av maskinlæringsmodeller, der gradienter er nødvendige for å optimalisere modellparametere.

Merk

I hovedsak er en gradient et sett med partiellderivert.

Bruk av Gradient Tape

For å bruke Gradient Tape, følg disse trinnene:

Opprett en Gradient Tape-blokk: bruk with tf.GradientTape() as tape:. Alle beregninger innenfor denne blokken blir sporet;
Definer beregningene: utfør operasjoner med tensorer innenfor blokken (for eksempel definer et fremoverpass i et nevralt nettverk);
Beregn gradienter: bruk tape.gradient(target, sources) for å kalkulere gradientene til målet med hensyn til kildene.

Enkel gradientberegning

Et enkelt eksempel for å forstå dette bedre.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Denne koden beregner gradienten til y = x^2 ved x = 3. Dette tilsvarer den partielle deriverte av y med hensyn til x.

Flere partielle deriverte

Når utdata påvirkes av flere innganger, kan en partiell derivasjon beregnes med hensyn til hver av disse inngangene (eller bare et utvalg av dem). Dette oppnås ved å oppgi en liste med variabler som parameteren sources.

Resultatet fra denne operasjonen vil være en tilsvarende liste med tensorer, der hver tensor representerer den partielle deriverte med hensyn til hver av variablene spesifisert i sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Denne koden beregner gradienten til funksjonen y = sum(x^2 + 2*z) for gitte verdier av x og z. I dette eksemplet vises gradienten til x som en 2D tensor, hvor hvert element tilsvarer den partielle deriverte av den respektive verdien i den opprinnelige x-matrisen.

Merknad

For ytterligere innsikt i Gradient Tape-funksjonalitet, inkludert høyere ordens deriverte og uthenting av Jacobimatrisen, se den offisielle TensorFlow-dokumentasjonen.

Oppgave

Swipe to start coding

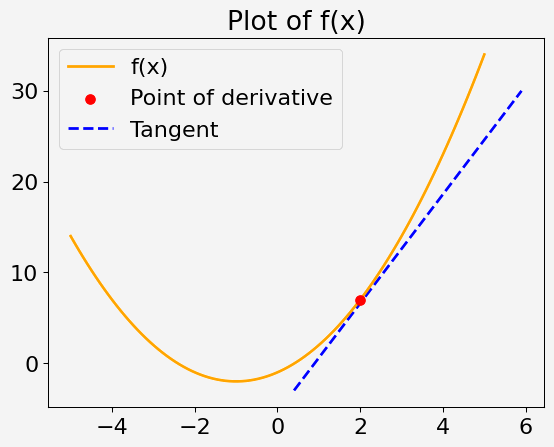
Målet ditt er å beregne gradienten (derivert) av en gitt matematisk funksjon i et spesifikt punkt ved hjelp av TensorFlows Gradient Tape. Funksjonen og punktet vil bli oppgitt, og du vil se hvordan du bruker TensorFlow for å finne gradienten i dette punktet.

Vurder en kvadratisk funksjon av én variabel x, definert som:

f(x) = x^2 + 2x - 1

Din oppgave er å beregne den deriverte av denne funksjonen ved x = 2.

Steg

Definer variabelen x i punktet der du ønsker å beregne den deriverte.
Bruk Gradient Tape for å registrere utregningen av funksjonen f(x).
Beregn gradienten til f(x) i det spesifiserte punktet.

Merk

Gradient kan kun beregnes for verdier av flyttallstype.

Løsning

Alt var klart?

Takk for tilbakemeldingene dine!

Seksjon 2. Kapittel 1

single

Spør AI

Spør om hva du vil, eller prøv ett av de foreslåtte spørsmålene for å starte chatten vår

Awesome!

Completion rate improved to 5.56

Sveip for å vise menyen