Gradient Tape

Compreender operações fundamentais com tensores permite avançar para a otimização e aceleração desses processos utilizando recursos integrados do TensorFlow. A primeira dessas ferramentas avançadas a ser explorada é o Gradient Tape.

O que é Gradient Tape?

Este capítulo aborda um dos conceitos fundamentais do TensorFlow, o Gradient Tape. Este recurso é essencial para a compreensão e implementação de técnicas de otimização baseada em gradientes, especialmente em deep learning.

O Gradient Tape no TensorFlow é uma ferramenta que registra operações para diferenciação automática. Quando operações são realizadas dentro de um bloco Gradient Tape, o TensorFlow acompanha todos os cálculos realizados. Isso é particularmente útil no treinamento de modelos de machine learning, onde os gradientes são necessários para otimizar os parâmetros do modelo.

Nota

Essencialmente, um gradiente é um conjunto de derivadas parciais.

Uso do Gradient Tape

Para utilizar o Gradient Tape, siga estes passos:

Crie um bloco Gradient Tape: utilize with tf.GradientTape() as tape:. Dentro deste bloco, todos os cálculos são rastreados;
Defina os cálculos: realize operações com tensores dentro do bloco (por exemplo, defina o passo de propagação direta de uma rede neural);
Calcule os gradientes: utilize tape.gradient(target, sources) para calcular os gradientes do alvo em relação às fontes.

Cálculo Simples de Gradiente

Um exemplo simples para melhor compreensão.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Este código calcula o gradiente de y = x^2 em x = 3. Isso é equivalente à derivada parcial de y em relação a x.

Várias Derivadas Parciais

Quando a saída é influenciada por múltiplas entradas, uma derivada parcial pode ser calculada em relação a cada uma dessas entradas (ou apenas algumas selecionadas). Isso é feito fornecendo uma lista de variáveis como parâmetro sources.

A saída dessa operação será uma lista correspondente de tensores, onde cada tensor representa a derivada parcial em relação a cada uma das variáveis especificadas em sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Este código calcula o gradiente da função y = sum(x^2 + 2*z) para valores dados de x e z. Neste exemplo, o gradiente de x é apresentado como um tensor 2D, onde cada elemento corresponde à derivada parcial do respectivo valor na matriz original x.

Nota

Para informações adicionais sobre as capacidades do Gradient Tape, incluindo derivadas de ordem superior e extração da matriz Jacobiana, consulte a documentação oficial do TensorFlow.

Tarefa

Swipe to start coding

Seu objetivo é calcular o gradiente (derivada) de uma determinada função matemática em um ponto específico utilizando o Gradient Tape do TensorFlow. A função e o ponto serão fornecidos, e você verá como usar o TensorFlow para encontrar o gradiente nesse ponto.

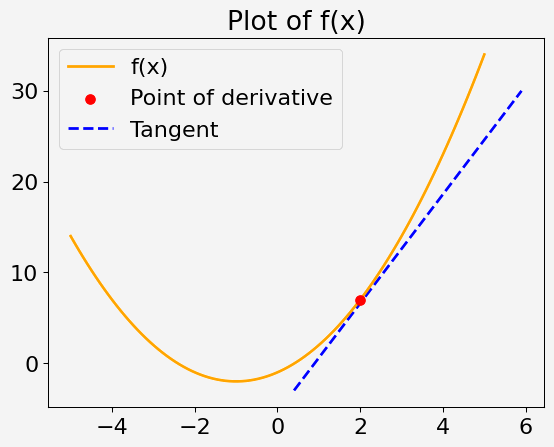
Considere uma função quadrática de uma única variável x, definida como:

f(x) = x^2 + 2x - 1

Sua tarefa é calcular a derivada dessa função em x = 2.

Etapas

Definir a variável x no ponto onde deseja calcular a derivada.
Utilizar o Gradient Tape para registrar o cálculo da função f(x).
Calcular o gradiente de f(x) no ponto especificado.

Observação

O gradiente só pode ser calculado para valores do tipo ponto flutuante.

Solução

Tudo estava claro?

Obrigado pelo seu feedback!

Seção 3. Capítulo 2

single

Pergunte à IA

Pergunte o que quiser ou experimente uma das perguntas sugeridas para iniciar nosso bate-papo

Suggested prompts:

Can you explain more about how Gradient Tape works in practice?

What are some common mistakes when using Gradient Tape?

Can you show an example of using Gradient Tape with a neural network?

Awesome!

Completion rate improved to 6.25

Deslize para mostrar o menu

Gradient Tape

O que é Gradient Tape?

Nota

Essencialmente, um gradiente é um conjunto de derivadas parciais.

Uso do Gradient Tape

Para utilizar o Gradient Tape, siga estes passos:

Crie um bloco Gradient Tape: utilize with tf.GradientTape() as tape:. Dentro deste bloco, todos os cálculos são rastreados;
Defina os cálculos: realize operações com tensores dentro do bloco (por exemplo, defina o passo de propagação direta de uma rede neural);
Calcule os gradientes: utilize tape.gradient(target, sources) para calcular os gradientes do alvo em relação às fontes.

Cálculo Simples de Gradiente

Um exemplo simples para melhor compreensão.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Este código calcula o gradiente de y = x^2 em x = 3. Isso é equivalente à derivada parcial de y em relação a x.

Várias Derivadas Parciais

A saída dessa operação será uma lista correspondente de tensores, onde cada tensor representa a derivada parcial em relação a cada uma das variáveis especificadas em sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Nota

Para informações adicionais sobre as capacidades do Gradient Tape, incluindo derivadas de ordem superior e extração da matriz Jacobiana, consulte a documentação oficial do TensorFlow.

Tarefa

Swipe to start coding

Considere uma função quadrática de uma única variável x, definida como:

f(x) = x^2 + 2x - 1

Sua tarefa é calcular a derivada dessa função em x = 2.

Etapas

Definir a variável x no ponto onde deseja calcular a derivada.
Utilizar o Gradient Tape para registrar o cálculo da função f(x).
Calcular o gradiente de f(x) no ponto especificado.

Observação

O gradiente só pode ser calculado para valores do tipo ponto flutuante.

Solução

Mude para o desktop para praticar no mundo realContinue de onde você está usando uma das opções abaixo

Tudo estava claro?

Obrigado pelo seu feedback!

Seção 3. Capítulo 2

single

Fitas de Gradiente

Gradient Tape

O que é Gradient Tape?

Uso do Gradient Tape

Cálculo Simples de Gradiente

Várias Derivadas Parciais

Etapas

Solução

Awesome!

Fitas de Gradiente

Gradient Tape

O que é Gradient Tape?

Uso do Gradient Tape

Cálculo Simples de Gradiente

Várias Derivadas Parciais

Etapas

Solução