Gradient Tape

Förståelse för grundläggande tensoroperationer möjliggör vidareutveckling mot att effektivisera och påskynda dessa processer med hjälp av inbyggda TensorFlow-funktioner. Det första av dessa avancerade verktyg att utforska är Gradient Tape.

Vad är Gradient Tape?

Detta kapitel behandlar ett av de grundläggande koncepten i TensorFlow, Gradient Tape. Denna funktion är avgörande för att förstå och implementera gradientbaserade optimeringstekniker, särskilt inom djupinlärning.

Gradient Tape i TensorFlow är ett verktyg som registrerar operationer för automatisk differentiering. När operationer utförs inom ett Gradient Tape-block spårar TensorFlow alla beräkningar som sker. Detta är särskilt användbart vid träning av maskininlärningsmodeller, där gradienter behövs för att optimera modellparametrar.

Notering

I grunden är en gradient en uppsättning partiella derivator.

Användning av Gradient Tape

För att använda Gradient Tape, följ dessa steg:

Skapa ett Gradient Tape-block: använd with tf.GradientTape() as tape:. Inom detta block spåras alla beräkningar;
Definiera beräkningarna: utför operationer med tensorer inom blocket (t.ex. definiera ett framåtpass av ett neuralt nätverk);
Beräkna gradienter: använd tape.gradient(target, sources) för att beräkna gradienterna av målet med avseende på källorna.

Enkel gradientberäkning

Ett enkelt exempel för att förstå detta bättre.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Denna kod beräknar gradienten av y = x^2 vid x = 3. Detta är detsamma som den partiella derivatan av y med avseende på x.

Flera partiella derivator

När utdata påverkas av flera indata kan en partiell derivata beräknas med avseende på var och en av dessa indata (eller bara ett urval). Detta uppnås genom att ange en lista av variabler som parametern sources.

Utdata från denna operation kommer att vara en motsvarande lista av tensorer, där varje tensor representerar den partiella derivatan med avseende på var och en av variablerna som anges i sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Denna kod beräknar gradienten av funktionen y = sum(x^2 + 2*z) för givna värden av x och z. I detta exempel visas gradienten av x som en 2D-tensor, där varje element motsvarar partiell derivata av respektive värde i den ursprungliga x-matrisen.

Notering

För ytterligare insikter om Gradient Tape-funktioner, inklusive högre ordningens derivator och extrahering av Jacobimatrisen, se den officiella TensorFlow-dokumentationen.

Uppgift

Swipe to start coding

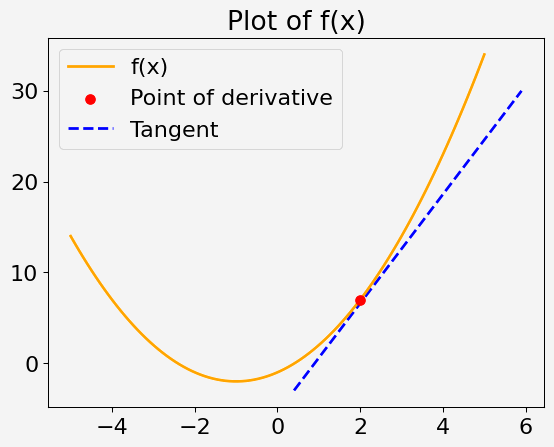
Målet är att beräkna derivatan (gradienten) av en given matematisk funktion vid en specificerad punkt med hjälp av TensorFlows Gradient Tape. Funktionen och punkten kommer att anges, och du får se hur TensorFlow används för att hitta gradienten vid den punkten.

Betrakta en kvadratisk funktion av en variabel x, definierad som:

f(x) = x^2 + 2x - 1

Din uppgift är att beräkna derivatan av denna funktion vid x = 2.

Steg

Definiera variabeln x vid den punkt där du vill beräkna derivatan.
Använd Gradient Tape för att spela in beräkningen av funktionen f(x).
Beräkna gradienten av f(x) vid den angivna punkten.

Observera

Gradient kan endast beräknas för värden av flyttalstyp.

Lösning

Var allt tydligt?

Tack för dina kommentarer!

Avsnitt 3. Kapitel 2

single

Fråga AI

Fråga vad du vill eller prova någon av de föreslagna frågorna för att starta vårt samtal

Suggested prompts:

Can you explain more about how Gradient Tape works in practice?

What are some common mistakes when using Gradient Tape?

Can you show an example of using Gradient Tape with a neural network?

Awesome!

Completion rate improved to 6.25

Svep för att visa menyn

Gradient Tape

Vad är Gradient Tape?

Notering

I grunden är en gradient en uppsättning partiella derivator.

Användning av Gradient Tape

För att använda Gradient Tape, följ dessa steg:

Skapa ett Gradient Tape-block: använd with tf.GradientTape() as tape:. Inom detta block spåras alla beräkningar;
Definiera beräkningarna: utför operationer med tensorer inom blocket (t.ex. definiera ett framåtpass av ett neuralt nätverk);
Beräkna gradienter: använd tape.gradient(target, sources) för att beräkna gradienterna av målet med avseende på källorna.

Enkel gradientberäkning

Ett enkelt exempel för att förstå detta bättre.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Denna kod beräknar gradienten av y = x^2 vid x = 3. Detta är detsamma som den partiella derivatan av y med avseende på x.

Flera partiella derivator


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Notering

För ytterligare insikter om Gradient Tape-funktioner, inklusive högre ordningens derivator och extrahering av Jacobimatrisen, se den officiella TensorFlow-dokumentationen.

Uppgift

Swipe to start coding

Betrakta en kvadratisk funktion av en variabel x, definierad som:

f(x) = x^2 + 2x - 1

Din uppgift är att beräkna derivatan av denna funktion vid x = 2.

Steg

Definiera variabeln x vid den punkt där du vill beräkna derivatan.
Använd Gradient Tape för att spela in beräkningen av funktionen f(x).
Beräkna gradienten av f(x) vid den angivna punkten.

Observera

Gradient kan endast beräknas för värden av flyttalstyp.

Lösning

Byt till skrivbordet för praktisk övningFortsätt där du är med ett av alternativen nedan

Var allt tydligt?

Tack för dina kommentarer!

Avsnitt 3. Kapitel 2

single