Gradient Tape

Розуміння базових операцій з тензорами дозволяє перейти до оптимізації та прискорення цих процесів за допомогою вбудованих можливостей TensorFlow. Першим із таких розширених інструментів для вивчення є Gradient Tape.

Що таке Gradient Tape?

У цьому розділі розглядається одна з основних концепцій у TensorFlow — Gradient Tape. Ця функція є ключовою для розуміння та реалізації методів оптимізації на основі градієнта, особливо у глибокому навчанні.

Gradient Tape у TensorFlow — це інструмент, який фіксує операції для автоматичного диференціювання. Коли операції виконуються всередині блоку Gradient Tape, TensorFlow відстежує всі обчислення, що відбуваються. Це особливо корисно під час навчання моделей машинного навчання, де градієнти необхідні для оптимізації параметрів моделі.

Примітка

По суті, градієнт — це набір часткових похідних.

Використання Gradient Tape

Щоб використовувати Gradient Tape, дотримуйтесь наступних кроків:

Створення блоку Gradient Tape: використовуйте with tf.GradientTape() as tape:. У цьому блоці всі обчислення відслідковуються;
Визначення обчислень: виконуйте операції з тензорами всередині блоку (наприклад, визначення прямого проходу нейронної мережі);
Обчислення градієнтів: використовуйте tape.gradient(target, sources), щоб обчислити градієнти цільової функції по відношенню до джерел.

Просте обчислення градієнта

Простий приклад для кращого розуміння.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Цей код обчислює градієнт y = x^2 при x = 3. Це те саме, що й часткова похідна y за x.

Кілька часткових похідних

Коли на вихід впливають декілька вхідних змінних, можна обчислити часткову похідну за кожною з цих змінних (або лише за вибраними). Це досягається шляхом передачі списку змінних як параметра sources.

Результатом цієї операції буде відповідний список тензорів, де кожен тензор представляє часткову похідну за кожною зі змінних, вказаних у sources.


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Цей код обчислює градієнт функції y = sum(x^2 + 2*z) для заданих значень x та z. У цьому прикладі градієнт x представлений як двовимірний тензор, де кожен елемент відповідає частинній похідній відповідного значення в початковій матриці x.

Примітка

Для додаткової інформації про можливості Gradient Tape, включаючи похідні вищих порядків та отримання матриці Якобі, зверніться до офіційної документації TensorFlow.

Завдання

Swipe to start coding

Ваша мета — обчислити градієнт (похідну) заданої математичної функції в зазначеній точці за допомогою Gradient Tape у TensorFlow. Функція та точка будуть надані, і ви побачите, як використовувати TensorFlow для знаходження градієнта в цій точці.

Розглянемо квадратичну функцію однієї змінної x, визначену як:

f(x) = x^2 + 2x - 1

Ваше завдання — обчислити похідну цієї функції при x = 2.

Кроки

Визначте змінну x у точці, в якій потрібно знайти похідну.
Використайте Gradient Tape для запису обчислення функції f(x).
Обчисліть градієнт f(x) у зазначеній точці.

Примітка

Градієнт можна обчислити лише для значень типу з плаваючою комою.

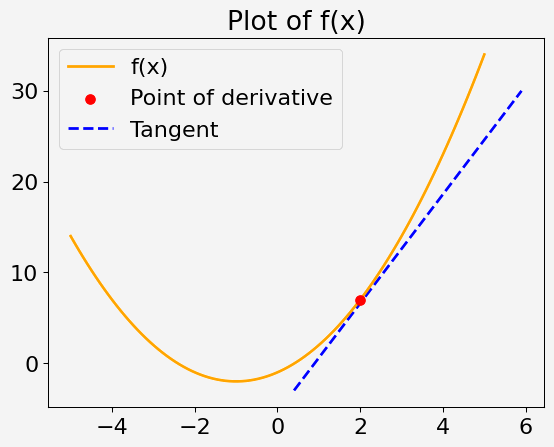
Рішення

Все було зрозуміло?

Дякуємо за ваш відгук!

Секція 3. Розділ 2

single

Запитати АІ

Запитайте про що завгодно або спробуйте одне із запропонованих запитань, щоб почати наш чат

Suggested prompts:

Can you explain more about how Gradient Tape works in practice?

What are some common mistakes when using Gradient Tape?

Can you show an example of using Gradient Tape with a neural network?

Awesome!

Completion rate improved to 6.25

Свайпніть щоб показати меню

Gradient Tape

Що таке Gradient Tape?

Примітка

По суті, градієнт — це набір часткових похідних.

Використання Gradient Tape

Щоб використовувати Gradient Tape, дотримуйтесь наступних кроків:

Створення блоку Gradient Tape: використовуйте with tf.GradientTape() as tape:. У цьому блоці всі обчислення відслідковуються;
Визначення обчислень: виконуйте операції з тензорами всередині блоку (наприклад, визначення прямого проходу нейронної мережі);
Обчислення градієнтів: використовуйте tape.gradient(target, sources), щоб обчислити градієнти цільової функції по відношенню до джерел.

Просте обчислення градієнта

Простий приклад для кращого розуміння.


              123456789101112131415
            
import tensorflow as tf

# Define input variables
x = tf.Variable(3.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = x * x
    
# Extract the gradient for the specific input (`x`)
grad = tape.gradient(y, x)

print(f'Result of y: {y}')
print(f'The gradient of y with respect to x is: {grad.numpy()}')

Цей код обчислює градієнт y = x^2 при x = 3. Це те саме, що й часткова похідна y за x.

Кілька часткових похідних


              1234567891011121314151617
            
import tensorflow as tf

# Define input variables
x = tf.Variable(tf.fill((2, 3), 3.0))
z = tf.Variable(5.0)

# Start recording the operations
with tf.GradientTape() as tape:
    # Define the calculations
    y = tf.reduce_sum(x * x + 2 * z)
    
# Extract the gradient for the specific inputs (`x` and `z`)
grad = tape.gradient(y, [x, z])

print(f'Result of y: {y}')
print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}")
print(f"The gradient of y with respect to z is: {grad[1].numpy()}")

Примітка

Завдання

Swipe to start coding

Розглянемо квадратичну функцію однієї змінної x, визначену як:

f(x) = x^2 + 2x - 1

Ваше завдання — обчислити похідну цієї функції при x = 2.

Кроки

Визначте змінну x у точці, в якій потрібно знайти похідну.
Використайте Gradient Tape для запису обчислення функції f(x).
Обчисліть градієнт f(x) у зазначеній точці.

Примітка

Градієнт можна обчислити лише для значень типу з плаваючою комою.

Рішення

Перейдіть на комп'ютер для реальної практикиПродовжуйте з того місця, де ви зупинились, використовуючи один з наведених нижче варіантів

Все було зрозуміло?

Дякуємо за ваш відгук!

Секція 3. Розділ 2

single

Градієнтна Стрічка

Gradient Tape

Що таке Gradient Tape?

Використання Gradient Tape

Просте обчислення градієнта

Кілька часткових похідних

Кроки

Рішення

Awesome!

Градієнтна Стрічка

Gradient Tape

Що таке Gradient Tape?

Використання Gradient Tape

Просте обчислення градієнта

Кілька часткових похідних

Кроки

Рішення