 Characteristics of Random Variables
Characteristics of Random Variables
Characteristics of random variables are important because they provide a formal way to describe and analyse the behaviour of uncertain events and outcomes in a probabilistic framework. They allow us to quantify and measure the uncertainty, variability, and central tendency of random variables, which are essential for making informed decisions and drawing meaningful conclusions from data.
The probability distribution of a random variable
The probability distribution of a random variable specifies the probabilities associated with each possible value in its domain. It can be represented using Probability Mass Function (PMF) for discrete random variables, or the Probability Density Function (PDF) for continuous random variables. We considered PMF and PDF in the previous chapter.
Let's look at the PDF of some continuous distributions:
123456789101112131415161718192021222324252627import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm, expon, chi2 # Create subplots with 1 row and 3 columns fig, axes = plt.subplots(1, 3) # Set figure size fig.set_size_inches(10, 5) # Generate evenly spaced values for x-axis x = np.linspace(0, 10, 500) # Plot PDF of standard normal distribution on the first subplot axes[0].plot(x, norm.pdf(x, loc=5, scale=2)) axes[0].set_title('Standard Normal Distribution') # Plot PDF of exponential distribution on the second subplot axes[1].plot(x, expon.pdf(x)) axes[1].set_title('Exponential Distribution') # Plot PDF of chi-square distribution on the third subplot axes[2].plot(x, chi2.pdf(x, df=3)) axes[2].set_title('Chi-square Distribution') # Show the plot plt.show()
Expected value
The expected value, also known as the mean or average, of a random variable is a measure of the central tendency of the random variable. It represents the weighted average of all possible values of the random variable, weighted by their respective probabilities.
Assume that X is discrete random variable and it's PMF looks like:
| Values | x_1 | x_2 | x_3 | .... | x_N |
|---|---|---|---|---|---|
| Probability | p_1 | p_2 | p_3 | .... | p_N |
We can calculate expectation as follows:
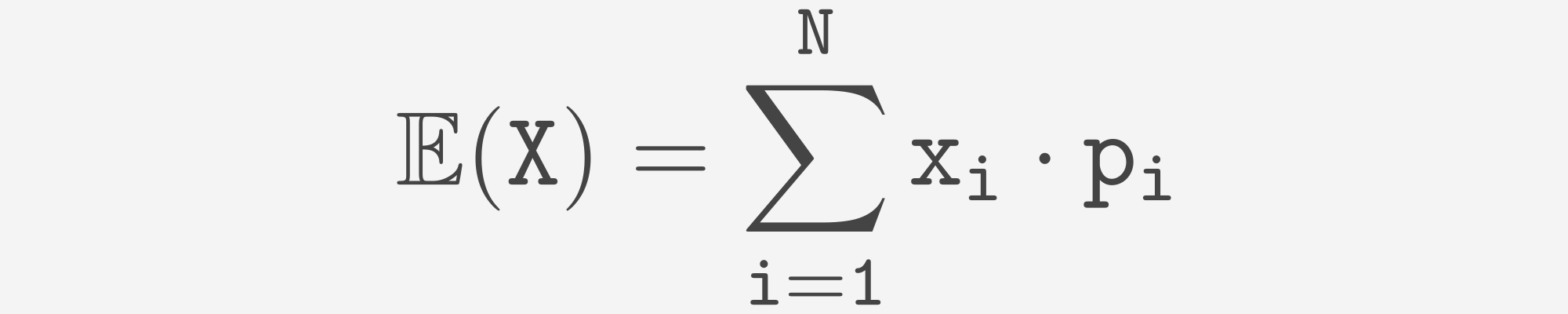
Now let's calculate expectation for continuous random variable X. Assuming, that f(x) if a PDF of this variable we can calculate expectation as follows:
Let's look at the PDF plot of normal distribution with different means:
1234567891011121314151617181920212223import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure object fig = plt.figure() # Set the size of the figure fig.set_size_inches(10, 5) # Generate evenly spaced values for the x-axis x = np.linspace(-10, 10, 500) # Plot three normal distributions with different means plt.plot(x, norm.pdf(x, loc=0, scale=2), label='Normal distribution with 0 mean') plt.plot(x, norm.pdf(x, loc=5, scale=2), label='Normal distribution with 5 mean') plt.plot(x, norm.pdf(x, loc=-5, scale=2), label='Normal distribution with -5 mean') # Add a legend to the plot plt.legend() # Show the plot plt.show()
Variance
The variance of a random variable is a measure of the dispersion or spread of the values of the random variable around its expected value. It quantifies the variability or uncertainty associated with the random variable. To calculate variance, we can use the following formula:
Let's look at the PDF plot of the normal distribution with different variances and fixed mean:
12345678910111213141516171819202122232425import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure with 1 row and 3 columns of subplots, sharing the y-axis fig, axes = plt.subplots(1, 3, sharey=True) # Set the overall size of the figure fig.set_size_inches(10, 5) # Generate 500 points evenly spaced between -10 and 10 x = np.linspace(-10, 10, 500) # Plot normal distributions with different variances (controlled by 'scale') on each subplot axes[0].plot(x, norm.pdf(x, loc=0, scale=1)) # Variance = 1 (scale = std. dev) axes[1].plot(x, norm.pdf(x, loc=0, scale=3)) # Variance = 9 (std. dev = 3) axes[2].plot(x, norm.pdf(x, loc=0, scale=5)) # Variance = 25 (std. dev = 5) # Set titles for each subplot to indicate the variance axes[0].set_title('Variance = 1') axes[1].set_title('Variance = 9') axes[2].set_title('Variance = 25') # Display the plot with all three distributions plt.show()
The square root of the variance is called standard deviation. Using standard deviation instead of variance can be advantageous due to two factors:
- We will work with smaller absolute values (while the variance will be, for example, 225, the standard deviation will be only 15, which is much more convenient in terms of calculations);
- The standard deviation is measured in the same units as the data, which can be important in certain cases (if, for example, we work with length in meters, then the variance will be measured in square meters, while the standard deviation is still in meters).
Note
The
scalekeyword of thescipy.stats.normclass represents the standard deviation of the normal distribution.
Thelockeyword of thescipy.stats.normclass represents the mean of the normal distribution.
Median
The median measures the central tendency in statistics that represents the middle value in a dataset when arranged in ascending or descending order.
We can calculate the median of random variable X as follows:
- Determine the CDF of
X; - Find the value y such that CDF(
y) =0.5; - This value y is the median of the random variable
X.
It's important to understand that expected value and median are two different characteristics: expected value is the weighted average of all possible values of the random variable, whereas the weights are the probabilities of those values occurring; on the other hand, the median is the value that separates the data into two halves.
For random variables with skewed distributions, this difference is the most significant.
Let's look at the example below:
12345678910111213141516171819202122232425262728293031323334353637import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # Create subplots fig, axes = plt.subplots(1, 2) fig.set_size_inches(10, 5) # Calculate the expected value and median for exponential distribution expected_value_exp = stats.expon.mean(scale=2) median_exp = stats.expon.median(scale=2) # Calculate the expected value and median for chi-square distribution expected_value_chi = stats.chi2.mean(df=3) median_chi = stats.chi2.median(df=3) # Generate x values for plotting PDFs x = np.linspace(0, 10, 500) # Plot the PDFs axes[0].plot(x, stats.expon.pdf(x, scale=2), label='Exponential PDF') axes[1].plot(x, stats.chi2.pdf(x, df=3), label='Chi-square PDF') # Plot vertical lines for expected value and median axes[0].axvline(expected_value_exp, color='red', linestyle='--', label='Expected Value') axes[0].axvline(median_exp, color='green', linestyle='--', label='Median') axes[1].axvline(expected_value_chi, color='red', linestyle='--', label='Expected Value') axes[1].axvline(median_chi, color='green', linestyle='--', label='Median') # Set titles and legends axes[0].set_title('Exponential PDF with Expected Value and Median') axes[1].set_title('Chi-square PDF with Expected Value and Median') axes[0].legend() axes[1].legend() # Show the plots plt.show()
We see that the expected value is shifted in the direction of the tail of the distribution. We have to admit that the expected value is more affected by outliers and anomalies, which makes this characteristic less reliable for real data analytics.
Thanks for your feedback!
Ask AI
Ask AI

Ask anything or try one of the suggested questions to begin our chat
Awesome!
Completion rate improved to 3.7 Characteristics of Random Variables
Characteristics of Random Variables
Swipe to show menu
Characteristics of random variables are important because they provide a formal way to describe and analyse the behaviour of uncertain events and outcomes in a probabilistic framework. They allow us to quantify and measure the uncertainty, variability, and central tendency of random variables, which are essential for making informed decisions and drawing meaningful conclusions from data.
The probability distribution of a random variable
The probability distribution of a random variable specifies the probabilities associated with each possible value in its domain. It can be represented using Probability Mass Function (PMF) for discrete random variables, or the Probability Density Function (PDF) for continuous random variables. We considered PMF and PDF in the previous chapter.
Let's look at the PDF of some continuous distributions:
123456789101112131415161718192021222324252627import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm, expon, chi2 # Create subplots with 1 row and 3 columns fig, axes = plt.subplots(1, 3) # Set figure size fig.set_size_inches(10, 5) # Generate evenly spaced values for x-axis x = np.linspace(0, 10, 500) # Plot PDF of standard normal distribution on the first subplot axes[0].plot(x, norm.pdf(x, loc=5, scale=2)) axes[0].set_title('Standard Normal Distribution') # Plot PDF of exponential distribution on the second subplot axes[1].plot(x, expon.pdf(x)) axes[1].set_title('Exponential Distribution') # Plot PDF of chi-square distribution on the third subplot axes[2].plot(x, chi2.pdf(x, df=3)) axes[2].set_title('Chi-square Distribution') # Show the plot plt.show()
Expected value
The expected value, also known as the mean or average, of a random variable is a measure of the central tendency of the random variable. It represents the weighted average of all possible values of the random variable, weighted by their respective probabilities.
Assume that X is discrete random variable and it's PMF looks like:
| Values | x_1 | x_2 | x_3 | .... | x_N |
|---|---|---|---|---|---|
| Probability | p_1 | p_2 | p_3 | .... | p_N |
We can calculate expectation as follows:
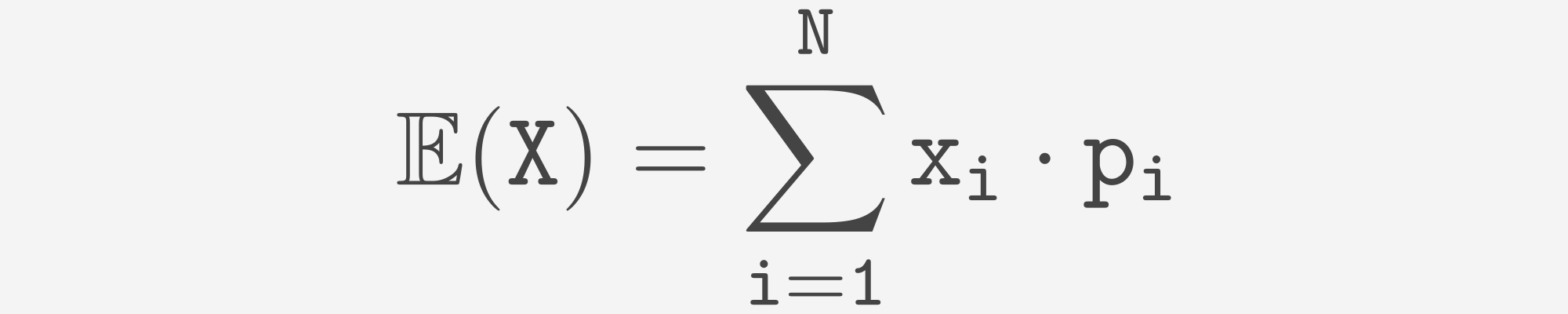
Now let's calculate expectation for continuous random variable X. Assuming, that f(x) if a PDF of this variable we can calculate expectation as follows:
Let's look at the PDF plot of normal distribution with different means:
1234567891011121314151617181920212223import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure object fig = plt.figure() # Set the size of the figure fig.set_size_inches(10, 5) # Generate evenly spaced values for the x-axis x = np.linspace(-10, 10, 500) # Plot three normal distributions with different means plt.plot(x, norm.pdf(x, loc=0, scale=2), label='Normal distribution with 0 mean') plt.plot(x, norm.pdf(x, loc=5, scale=2), label='Normal distribution with 5 mean') plt.plot(x, norm.pdf(x, loc=-5, scale=2), label='Normal distribution with -5 mean') # Add a legend to the plot plt.legend() # Show the plot plt.show()
Variance
The variance of a random variable is a measure of the dispersion or spread of the values of the random variable around its expected value. It quantifies the variability or uncertainty associated with the random variable. To calculate variance, we can use the following formula:
Let's look at the PDF plot of the normal distribution with different variances and fixed mean:
12345678910111213141516171819202122232425import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure with 1 row and 3 columns of subplots, sharing the y-axis fig, axes = plt.subplots(1, 3, sharey=True) # Set the overall size of the figure fig.set_size_inches(10, 5) # Generate 500 points evenly spaced between -10 and 10 x = np.linspace(-10, 10, 500) # Plot normal distributions with different variances (controlled by 'scale') on each subplot axes[0].plot(x, norm.pdf(x, loc=0, scale=1)) # Variance = 1 (scale = std. dev) axes[1].plot(x, norm.pdf(x, loc=0, scale=3)) # Variance = 9 (std. dev = 3) axes[2].plot(x, norm.pdf(x, loc=0, scale=5)) # Variance = 25 (std. dev = 5) # Set titles for each subplot to indicate the variance axes[0].set_title('Variance = 1') axes[1].set_title('Variance = 9') axes[2].set_title('Variance = 25') # Display the plot with all three distributions plt.show()
The square root of the variance is called standard deviation. Using standard deviation instead of variance can be advantageous due to two factors:
- We will work with smaller absolute values (while the variance will be, for example, 225, the standard deviation will be only 15, which is much more convenient in terms of calculations);
- The standard deviation is measured in the same units as the data, which can be important in certain cases (if, for example, we work with length in meters, then the variance will be measured in square meters, while the standard deviation is still in meters).
Note
The
scalekeyword of thescipy.stats.normclass represents the standard deviation of the normal distribution.
Thelockeyword of thescipy.stats.normclass represents the mean of the normal distribution.
Median
The median measures the central tendency in statistics that represents the middle value in a dataset when arranged in ascending or descending order.
We can calculate the median of random variable X as follows:
- Determine the CDF of
X; - Find the value y such that CDF(
y) =0.5; - This value y is the median of the random variable
X.
It's important to understand that expected value and median are two different characteristics: expected value is the weighted average of all possible values of the random variable, whereas the weights are the probabilities of those values occurring; on the other hand, the median is the value that separates the data into two halves.
For random variables with skewed distributions, this difference is the most significant.
Let's look at the example below:
12345678910111213141516171819202122232425262728293031323334353637import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # Create subplots fig, axes = plt.subplots(1, 2) fig.set_size_inches(10, 5) # Calculate the expected value and median for exponential distribution expected_value_exp = stats.expon.mean(scale=2) median_exp = stats.expon.median(scale=2) # Calculate the expected value and median for chi-square distribution expected_value_chi = stats.chi2.mean(df=3) median_chi = stats.chi2.median(df=3) # Generate x values for plotting PDFs x = np.linspace(0, 10, 500) # Plot the PDFs axes[0].plot(x, stats.expon.pdf(x, scale=2), label='Exponential PDF') axes[1].plot(x, stats.chi2.pdf(x, df=3), label='Chi-square PDF') # Plot vertical lines for expected value and median axes[0].axvline(expected_value_exp, color='red', linestyle='--', label='Expected Value') axes[0].axvline(median_exp, color='green', linestyle='--', label='Median') axes[1].axvline(expected_value_chi, color='red', linestyle='--', label='Expected Value') axes[1].axvline(median_chi, color='green', linestyle='--', label='Median') # Set titles and legends axes[0].set_title('Exponential PDF with Expected Value and Median') axes[1].set_title('Chi-square PDF with Expected Value and Median') axes[0].legend() axes[1].legend() # Show the plots plt.show()
We see that the expected value is shifted in the direction of the tail of the distribution. We have to admit that the expected value is more affected by outliers and anomalies, which makes this characteristic less reliable for real data analytics.
Thanks for your feedback!