 Eigenschaften von Zufallsvariablen
Eigenschaften von Zufallsvariablen
Die Eigenschaften von Zufallsvariablen sind wichtig, weil sie eine formale Möglichkeit bieten, das Verhalten unsicherer Ereignisse und Ergebnisse in einem probabilistischen Rahmen zu beschreiben und zu analysieren. Sie ermöglichen es uns, die Unsicherheit, Variabilität und zentrale Tendenz von Zufallsvariablen zu quantifizieren und messen, was entscheidend ist, um fundierte Entscheidungen zu treffen und aussagekräftige Schlussfolgerungen aus Daten zu ziehen.
Die Wahrscheinlichkeitsverteilung einer Zufallsvariablen
Die Wahrscheinlichkeitsverteilung einer Zufallsvariablen gibt die Wahrscheinlichkeiten an, die mit jedem möglichen Wert in ihrem Bereich verbunden sind. Sie kann durch die Wahrscheinlichkeitsmassenfunktion (PMF) für diskrete Zufallsvariablen oder die Wahrscheinlichkeitsdichtefunktion (PDF) für kontinuierliche Zufallsvariablen dargestellt werden. Wir haben PMF und PDF im vorherigen Kapitel betrachtet.
Schauen wir uns die PDF einiger kontinuierlicher Verteilungen an:
123456789101112131415161718192021222324252627import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm, expon, chi2 # Create subplots with 1 row and 3 columns fig, axes = plt.subplots(1, 3) # Set figure size fig.set_size_inches(10, 5) # Generate evenly spaced values for x-axis x = np.linspace(0, 10, 500) # Plot PDF of standard normal distribution on the first subplot axes[0].plot(x, norm.pdf(x, loc=5, scale=2)) axes[0].set_title('Standard Normal Distribution') # Plot PDF of exponential distribution on the second subplot axes[1].plot(x, expon.pdf(x)) axes[1].set_title('Exponential Distribution') # Plot PDF of chi-square distribution on the third subplot axes[2].plot(x, chi2.pdf(x, df=3)) axes[2].set_title('Chi-square Distribution') # Show the plot plt.show()
Erwartungswert
Der Erwartungswert, auch bekannt als Mittelwert oder Durchschnitt, einer Zufallsvariablen ist ein Maß für die zentrale Tendenz der Zufallsvariablen. Er repräsentiert den gewichteten Durchschnitt aller möglichen Werte der Zufallsvariablen, gewichtet nach ihren jeweiligen Wahrscheinlichkeiten.
Angenommen, X ist eine diskrete Zufallsvariable und ihre PMF sieht folgendermaßen aus:
| Werte | x_1 | x_2 | x_3 | .... | x_N |
|---|---|---|---|---|---|
| Wahrscheinlichkeit | p_1 | p_2 | p_3 | .... | p_N |
Wir können die Erwartung wie folgt berechnen:
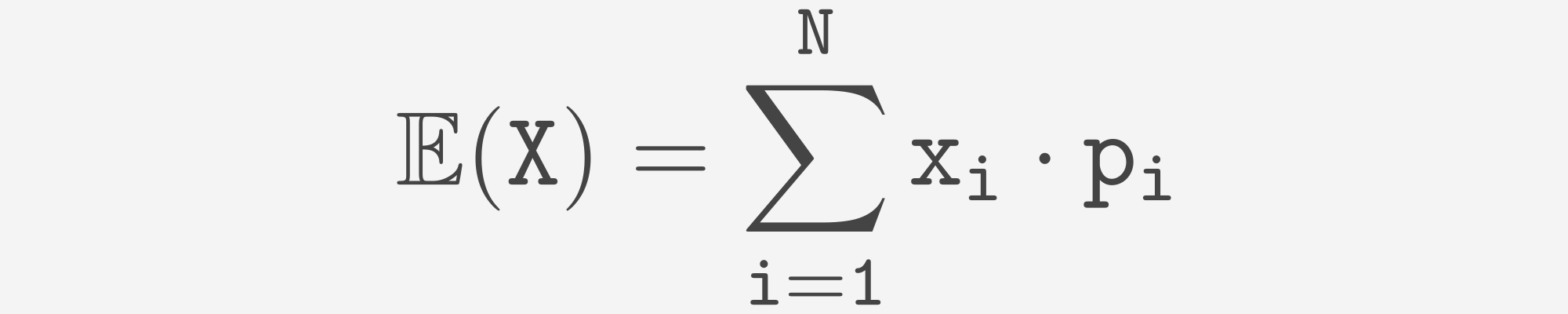
Nun berechnen wir die Erwartung für die kontinuierliche Zufallsvariable X. Angenommen, f(x) ist eine PDF dieser Variablen, können wir die Erwartung wie folgt berechnen:
Schauen wir uns das PDF-Diagramm der Normalverteilung mit unterschiedlichen Mittelwerten an:
1234567891011121314151617181920212223import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure object fig = plt.figure() # Set the size of the figure fig.set_size_inches(10, 5) # Generate evenly spaced values for the x-axis x = np.linspace(-10, 10, 500) # Plot three normal distributions with different means plt.plot(x, norm.pdf(x, loc=0, scale=2), label='Normal distribution with 0 mean') plt.plot(x, norm.pdf(x, loc=5, scale=2), label='Normal distribution with 5 mean') plt.plot(x, norm.pdf(x, loc=-5, scale=2), label='Normal distribution with -5 mean') # Add a legend to the plot plt.legend() # Show the plot plt.show()
Varianz
Die Varianz einer Zufallsvariablen ist ein Maß für die Streuung oder Verteilung der Werte der Zufallsvariablen um ihren Erwartungswert. Sie quantifiziert die Variabilität oder Unsicherheit, die mit der Zufallsvariablen verbunden ist. Um die Varianz zu berechnen, können wir die folgende Formel verwenden:
Betrachten wir das PDF-Diagramm der Normalverteilung mit unterschiedlichen Varianzen und festem Mittelwert:
12345678910111213141516171819202122232425import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure with 1 row and 3 columns of subplots, sharing the y-axis fig, axes = plt.subplots(1, 3, sharey=True) # Set the overall size of the figure fig.set_size_inches(10, 5) # Generate 500 points evenly spaced between -10 and 10 x = np.linspace(-10, 10, 500) # Plot normal distributions with different variances (controlled by 'scale') on each subplot axes[0].plot(x, norm.pdf(x, loc=0, scale=1)) # Variance = 1 (scale = std. dev) axes[1].plot(x, norm.pdf(x, loc=0, scale=3)) # Variance = 9 (std. dev = 3) axes[2].plot(x, norm.pdf(x, loc=0, scale=5)) # Variance = 25 (std. dev = 5) # Set titles for each subplot to indicate the variance axes[0].set_title('Variance = 1') axes[1].set_title('Variance = 9') axes[2].set_title('Variance = 25') # Display the plot with all three distributions plt.show()
Die Quadratwurzel der Varianz wird als Standardabweichung bezeichnet. Die Verwendung der Standardabweichung anstelle der Varianz kann aufgrund zweier Faktoren vorteilhaft sein:
- Wir arbeiten mit kleineren absoluten Werten (während die Varianz beispielsweise 225 beträgt, beträgt die Standardabweichung nur 15, was in Bezug auf Berechnungen viel praktischer ist);
- Die Standardabweichung wird in denselben Einheiten wie die Daten gemessen, was in bestimmten Fällen wichtig sein kann (wenn wir beispielsweise mit Längen in Metern arbeiten, wird die Varianz in Quadratmetern gemessen, während die Standardabweichung weiterhin in Metern ist).
Hinweis
Das
scale-Schlüsselwort derscipy.stats.norm-Klasse repräsentiert die Standardabweichung der Normalverteilung.
Dasloc-Schlüsselwort derscipy.stats.norm-Klasse repräsentiert den Mittelwert der Normalverteilung.
Median
Der Median misst die zentrale Tendenz in der Statistik, die den mittleren Wert in einem Datensatz darstellt, wenn dieser in aufsteigender oder absteigender Reihenfolge angeordnet ist.
Wir können den Median der Zufallsvariablen X wie folgt berechnen:
- Bestimmen Sie die CDF von
X; - Finden Sie den Wert y, sodass CDF(
y) =0.5; - Dieser Wert y ist der Median der Zufallsvariablen
X.
Es ist wichtig zu verstehen, dass Erwartungswert und Median zwei unterschiedliche Merkmale sind: Der Erwartungswert ist der gewichtete Durchschnitt aller möglichen Werte der Zufallsvariablen, wobei die Gewichte die Wahrscheinlichkeiten des Auftretens dieser Werte sind; andererseits ist der Median der Wert, der die Daten in zwei Hälften teilt.
Für Zufallsvariablen mit schiefen Verteilungen ist dieser Unterschied am bedeutendsten.
Schauen wir uns das folgende Beispiel an:
12345678910111213141516171819202122232425262728293031323334353637import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # Create subplots fig, axes = plt.subplots(1, 2) fig.set_size_inches(10, 5) # Calculate the expected value and median for exponential distribution expected_value_exp = stats.expon.mean(scale=2) median_exp = stats.expon.median(scale=2) # Calculate the expected value and median for chi-square distribution expected_value_chi = stats.chi2.mean(df=3) median_chi = stats.chi2.median(df=3) # Generate x values for plotting PDFs x = np.linspace(0, 10, 500) # Plot the PDFs axes[0].plot(x, stats.expon.pdf(x, scale=2), label='Exponential PDF') axes[1].plot(x, stats.chi2.pdf(x, df=3), label='Chi-square PDF') # Plot vertical lines for expected value and median axes[0].axvline(expected_value_exp, color='red', linestyle='--', label='Expected Value') axes[0].axvline(median_exp, color='green', linestyle='--', label='Median') axes[1].axvline(expected_value_chi, color='red', linestyle='--', label='Expected Value') axes[1].axvline(median_chi, color='green', linestyle='--', label='Median') # Set titles and legends axes[0].set_title('Exponential PDF with Expected Value and Median') axes[1].set_title('Chi-square PDF with Expected Value and Median') axes[0].legend() axes[1].legend() # Show the plots plt.show()
Wir sehen, dass der Erwartungswert in Richtung des Endes der Verteilung verschoben ist. Wir müssen zugeben, dass der Erwartungswert stärker von Ausreißern und Anomalien beeinflusst wird, was diese Eigenschaft für die Analyse realer Daten weniger zuverlässig macht.
Danke für Ihr Feedback!
Fragen Sie AI
Fragen Sie AI

Fragen Sie alles oder probieren Sie eine der vorgeschlagenen Fragen, um unser Gespräch zu beginnen
Großartig!
Completion Rate verbessert auf 3.7 Eigenschaften von Zufallsvariablen
Eigenschaften von Zufallsvariablen
Swipe um das Menü anzuzeigen
Die Eigenschaften von Zufallsvariablen sind wichtig, weil sie eine formale Möglichkeit bieten, das Verhalten unsicherer Ereignisse und Ergebnisse in einem probabilistischen Rahmen zu beschreiben und zu analysieren. Sie ermöglichen es uns, die Unsicherheit, Variabilität und zentrale Tendenz von Zufallsvariablen zu quantifizieren und messen, was entscheidend ist, um fundierte Entscheidungen zu treffen und aussagekräftige Schlussfolgerungen aus Daten zu ziehen.
Die Wahrscheinlichkeitsverteilung einer Zufallsvariablen
Die Wahrscheinlichkeitsverteilung einer Zufallsvariablen gibt die Wahrscheinlichkeiten an, die mit jedem möglichen Wert in ihrem Bereich verbunden sind. Sie kann durch die Wahrscheinlichkeitsmassenfunktion (PMF) für diskrete Zufallsvariablen oder die Wahrscheinlichkeitsdichtefunktion (PDF) für kontinuierliche Zufallsvariablen dargestellt werden. Wir haben PMF und PDF im vorherigen Kapitel betrachtet.
Schauen wir uns die PDF einiger kontinuierlicher Verteilungen an:
123456789101112131415161718192021222324252627import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm, expon, chi2 # Create subplots with 1 row and 3 columns fig, axes = plt.subplots(1, 3) # Set figure size fig.set_size_inches(10, 5) # Generate evenly spaced values for x-axis x = np.linspace(0, 10, 500) # Plot PDF of standard normal distribution on the first subplot axes[0].plot(x, norm.pdf(x, loc=5, scale=2)) axes[0].set_title('Standard Normal Distribution') # Plot PDF of exponential distribution on the second subplot axes[1].plot(x, expon.pdf(x)) axes[1].set_title('Exponential Distribution') # Plot PDF of chi-square distribution on the third subplot axes[2].plot(x, chi2.pdf(x, df=3)) axes[2].set_title('Chi-square Distribution') # Show the plot plt.show()
Erwartungswert
Der Erwartungswert, auch bekannt als Mittelwert oder Durchschnitt, einer Zufallsvariablen ist ein Maß für die zentrale Tendenz der Zufallsvariablen. Er repräsentiert den gewichteten Durchschnitt aller möglichen Werte der Zufallsvariablen, gewichtet nach ihren jeweiligen Wahrscheinlichkeiten.
Angenommen, X ist eine diskrete Zufallsvariable und ihre PMF sieht folgendermaßen aus:
| Werte | x_1 | x_2 | x_3 | .... | x_N |
|---|---|---|---|---|---|
| Wahrscheinlichkeit | p_1 | p_2 | p_3 | .... | p_N |
Wir können die Erwartung wie folgt berechnen:
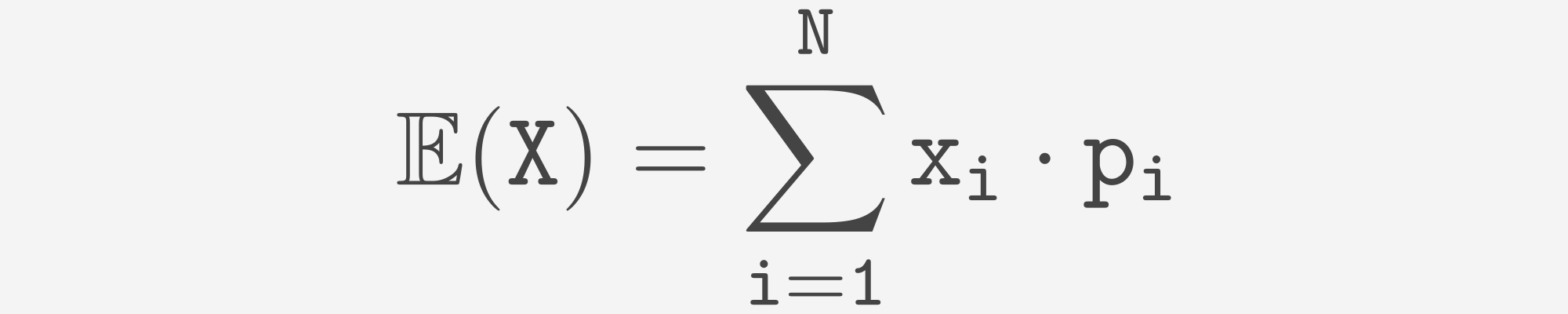
Nun berechnen wir die Erwartung für die kontinuierliche Zufallsvariable X. Angenommen, f(x) ist eine PDF dieser Variablen, können wir die Erwartung wie folgt berechnen:
Schauen wir uns das PDF-Diagramm der Normalverteilung mit unterschiedlichen Mittelwerten an:
1234567891011121314151617181920212223import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure object fig = plt.figure() # Set the size of the figure fig.set_size_inches(10, 5) # Generate evenly spaced values for the x-axis x = np.linspace(-10, 10, 500) # Plot three normal distributions with different means plt.plot(x, norm.pdf(x, loc=0, scale=2), label='Normal distribution with 0 mean') plt.plot(x, norm.pdf(x, loc=5, scale=2), label='Normal distribution with 5 mean') plt.plot(x, norm.pdf(x, loc=-5, scale=2), label='Normal distribution with -5 mean') # Add a legend to the plot plt.legend() # Show the plot plt.show()
Varianz
Die Varianz einer Zufallsvariablen ist ein Maß für die Streuung oder Verteilung der Werte der Zufallsvariablen um ihren Erwartungswert. Sie quantifiziert die Variabilität oder Unsicherheit, die mit der Zufallsvariablen verbunden ist. Um die Varianz zu berechnen, können wir die folgende Formel verwenden:
Betrachten wir das PDF-Diagramm der Normalverteilung mit unterschiedlichen Varianzen und festem Mittelwert:
12345678910111213141516171819202122232425import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure with 1 row and 3 columns of subplots, sharing the y-axis fig, axes = plt.subplots(1, 3, sharey=True) # Set the overall size of the figure fig.set_size_inches(10, 5) # Generate 500 points evenly spaced between -10 and 10 x = np.linspace(-10, 10, 500) # Plot normal distributions with different variances (controlled by 'scale') on each subplot axes[0].plot(x, norm.pdf(x, loc=0, scale=1)) # Variance = 1 (scale = std. dev) axes[1].plot(x, norm.pdf(x, loc=0, scale=3)) # Variance = 9 (std. dev = 3) axes[2].plot(x, norm.pdf(x, loc=0, scale=5)) # Variance = 25 (std. dev = 5) # Set titles for each subplot to indicate the variance axes[0].set_title('Variance = 1') axes[1].set_title('Variance = 9') axes[2].set_title('Variance = 25') # Display the plot with all three distributions plt.show()
Die Quadratwurzel der Varianz wird als Standardabweichung bezeichnet. Die Verwendung der Standardabweichung anstelle der Varianz kann aufgrund zweier Faktoren vorteilhaft sein:
- Wir arbeiten mit kleineren absoluten Werten (während die Varianz beispielsweise 225 beträgt, beträgt die Standardabweichung nur 15, was in Bezug auf Berechnungen viel praktischer ist);
- Die Standardabweichung wird in denselben Einheiten wie die Daten gemessen, was in bestimmten Fällen wichtig sein kann (wenn wir beispielsweise mit Längen in Metern arbeiten, wird die Varianz in Quadratmetern gemessen, während die Standardabweichung weiterhin in Metern ist).
Hinweis
Das
scale-Schlüsselwort derscipy.stats.norm-Klasse repräsentiert die Standardabweichung der Normalverteilung.
Dasloc-Schlüsselwort derscipy.stats.norm-Klasse repräsentiert den Mittelwert der Normalverteilung.
Median
Der Median misst die zentrale Tendenz in der Statistik, die den mittleren Wert in einem Datensatz darstellt, wenn dieser in aufsteigender oder absteigender Reihenfolge angeordnet ist.
Wir können den Median der Zufallsvariablen X wie folgt berechnen:
- Bestimmen Sie die CDF von
X; - Finden Sie den Wert y, sodass CDF(
y) =0.5; - Dieser Wert y ist der Median der Zufallsvariablen
X.
Es ist wichtig zu verstehen, dass Erwartungswert und Median zwei unterschiedliche Merkmale sind: Der Erwartungswert ist der gewichtete Durchschnitt aller möglichen Werte der Zufallsvariablen, wobei die Gewichte die Wahrscheinlichkeiten des Auftretens dieser Werte sind; andererseits ist der Median der Wert, der die Daten in zwei Hälften teilt.
Für Zufallsvariablen mit schiefen Verteilungen ist dieser Unterschied am bedeutendsten.
Schauen wir uns das folgende Beispiel an:
12345678910111213141516171819202122232425262728293031323334353637import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # Create subplots fig, axes = plt.subplots(1, 2) fig.set_size_inches(10, 5) # Calculate the expected value and median for exponential distribution expected_value_exp = stats.expon.mean(scale=2) median_exp = stats.expon.median(scale=2) # Calculate the expected value and median for chi-square distribution expected_value_chi = stats.chi2.mean(df=3) median_chi = stats.chi2.median(df=3) # Generate x values for plotting PDFs x = np.linspace(0, 10, 500) # Plot the PDFs axes[0].plot(x, stats.expon.pdf(x, scale=2), label='Exponential PDF') axes[1].plot(x, stats.chi2.pdf(x, df=3), label='Chi-square PDF') # Plot vertical lines for expected value and median axes[0].axvline(expected_value_exp, color='red', linestyle='--', label='Expected Value') axes[0].axvline(median_exp, color='green', linestyle='--', label='Median') axes[1].axvline(expected_value_chi, color='red', linestyle='--', label='Expected Value') axes[1].axvline(median_chi, color='green', linestyle='--', label='Median') # Set titles and legends axes[0].set_title('Exponential PDF with Expected Value and Median') axes[1].set_title('Chi-square PDF with Expected Value and Median') axes[0].legend() axes[1].legend() # Show the plots plt.show()
Wir sehen, dass der Erwartungswert in Richtung des Endes der Verteilung verschoben ist. Wir müssen zugeben, dass der Erwartungswert stärker von Ausreißern und Anomalien beeinflusst wird, was diese Eigenschaft für die Analyse realer Daten weniger zuverlässig macht.
Danke für Ihr Feedback!